The situation is measuring the temperature of a buried sensor situated at some distance below the surface after an impulse of thermal energy is applied. The physics solution to this problem is the heat kernel function which is the impulse response or Green's function for that variation of the master equation. This is pure diffusion with no convection involved (heat is not sensitive to fields, gravity or electrical, so no convection).
However the diffusion coefficient involved in the solution is not known to any degree of precision. The earthen material that the heat is diffusing through is heterogeneously disordered, and all we can really guess at that it has a mean value for the diffusion coefficient. By inferring through the maximum entropy principle, we can say that the diffusion coefficient has a PDF that is exponentially distributed with a mean value D.
We then work the original heat equation solution with this smeared version of D, and then the kernel simplifies to a exp() solution.
$$ {1\over{2\sqrt{Dt}}}e^{-x/\sqrt{Dt}} $$
But we also don't know the value of x that well and have uncertainty in its value. If we give a Maximum Entropy uncertainty in that value, then the solution simpilfies to
$$ {1\over2}{1\over{x_0+\sqrt{Dt}}} $$
where x0 is a smeared value for x.
This is a valid approximation to the solution of this particular problem and the following Figure 1 is a fit to experimental data. There are two parameters to the model, an asymptotic value that is used to extrapolate a steady state value based on the initial thermal impulse and the smearing value which generates the red line. The slightly noisy blue line is the data, and one can note the good agreement.
 |
| Figure 1: Fit of thermal dispersive diffusion model (red) to a heat impulse response (blue). |
By changing an effective scaled diffusion coefficient from small to large, we can change the tail substantially, see Figure 2. We call it effective because the stochastic smearing on D and Length makes it scale-free and we can longer tell if the mean in D or Length is greater. We could have a huge mean for D and a small mean for Length, or vice versa, but we could not distinguish between the cases, unless we have measurements at more locations.
 |
| Figure 2 : Impulse response with increasing diffusion coefficient top to bottom. The term x represents time, not position . |
The integral shows how the heat sink target transiently draws heat from the source. If the effective diffusion coefficient is very small, an outlet for heat dispersal does not exist and the temperature will continue to rise. If the diffusion coefficient is zero, then the temperature will increase linearly with time, t (again this is without a radiative response to provide an outlet).
 |
| Figure 3 : Unit step response of dispersed thermal diffusion. The smaller the effective thermal diffusion coefficient, the longer the heat can stay near the source. |
Eventually the response will attain a square root growth law, indicative of a Fick's law regime of what is often referred to as parabolic growth (somewhat of a misnomer). The larger the diffusion coefficient, the more that the response will diverge from the linear growth. All this means is that the heat is dispersively diffusing to the heat sink.
Application to AGW
This has implications for the "heat in the pipeline" scenario of increasing levels of greenhouse gases and the expected warming of the planet. Since the heat content of the oceans are about 1200 times that of the atmosphere, it is expected that a significant portion of the heat will enter the oceans, where the large volume of water will act as a heat sink. This heat becomes hard to detect because of the ocean's large heat capacity; and it will take time for the climate researchers to integrate the measurements before they can conclusively demonstrate that diffusion path.
In the meantime, the lower atmospheric temperature may not change as much as it could, because the GHG heat gets diverted to the oceans. The heat is therefore "in the pipeline", with the ocean acting as a buffer, capturing the heat that would immediately appear in the atmosphere in the absence of such a large heat sink. The practical evidence for this is a slowing of the atmospheric temperature rise, in accordance with the slower sqrt(t) rise than the linear t. However, this can only go on so long, and when the ocean's heat sink provides a smaller temperature difference than the atmosphere, the excess heat will cause a more immediate temperature rise nearer the source, instead of being spread around.
In terms of AGW, whenever the global temperature measurements start to show divergence from the model, it is likely due to the ocean's heat capacity. Like the atmospheric CO2, the excess heat is not "missing" but merely spread around.
EDIT:
The contents of this post are discussed on The Missing Heat isn't Missing at all.
I mentioned in comments that the analogy is very close to sizing a heat sink for your computer’s CPU. The heat sink works up to a point, then the fan takes over to dissipate that buffered heat via the fins. The problem is that the planet does not have a fan nor fins, but it does have an ocean as a sink. The excess heat then has nowhere left to go. Eventually the heat flow reaches a steady state, and the pipelining or buffering fails to dissipate the excess heat.
What's fittingly apropos is the unification of the two "missing" cases of climate science.
1. The "missing" CO2. Skeptics often complain about the missing CO2 in atmospheric measurements from that anticipated based on fossil fuel emissions. About 40% was missing by most accounts. This lead to confusion between the ideas of residence times versus adjustment times of atmospheric CO2. As it turns out, a simple model of CO2 diffusing to sequestering sites accurately represented the long adjustment times and the diffusion tails account for the missing 40%. I derived this phenomenon using diffusion of trace molecules, while most climate scientists apply a range of time constants that approximate diffusion.
2. The "missing" heat. Concerns also arise about missing heat based on measurements of the average global temperature. When a TCR/ECS* ratio of 0.56 is asserted, 44% of the heat is missing. This leads to confusion about where the heat is in the pipeline. As it turns out, a simple model of thermal energy diffusing to deeper ocean sites may account for the missing 44%. In this post, I derived this using a master heat equation and uncertainty in the parameters. Isaac Held uses a different approach based on time constants.
So that is the basic idea behind modeling the missing quantities of CO2 and of heat -- just apply a mechanism of dispersed diffusion. For CO2, this is the Fokker-Planck equation and for temperature, the heat equation. By applying diffusion principles, the solution arguably comes out much more cleanly and it will lead to better intuition as to the actual physics behind the observed behaviors.
I was alerted to this paper by Hansen et al (1985) which uses a box diffusion model. Hansen’s Figure 2 looks just like my Figure 3 above. This bends over just like Hansen’s does due to the diffusive square root of time dependence. When superimposed, it is not quite as strong a bend as shown in Figure 4 below.
 |
| Figure 4: Comparison against Hansen's model of diffusion |
This missing heat is now clarified in my mind. In the paper Hansen calls it “unrealized warming”, which is heat entering into the ocean without raising the climate temperature substantially.
EDIT:
The following figure is a guide to the eye which explains the role of the ocean in short- and long-term thermal diffusion, i.e. transient climate response. The data from BEST illustrates the atmospheric-land temperatures, which are part of the fast response to the GHG forcing function. While the GISTEMP temperature data reflects more of the ocean's slow response.
 |
| Figure 5: Transient Climate Response explanation |
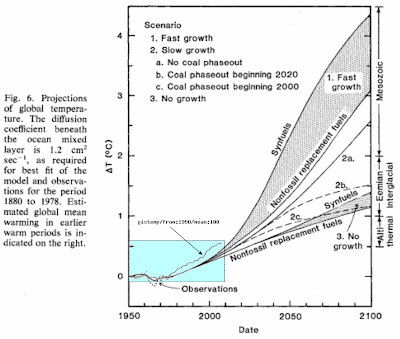 |
| Figure 6: Hansen's original projection of transient climate sensitivity plotted against the GISTEMP data, which factors in ocean surface temperatures. |
*
TCR = Transient Climate Response
ECS = Equilibrium Climate Sensitivity
Added:
"Somewhere around 23 x 10^22 Joules of energy over the past 40 years has gone into the top 2000m of the ocean due to the Earth’s energy imbalance "
That is an amazing number. If one assumes an energy imbalance of 1 watt/m^2, and integrate this over 40 years and over the areal cross-section of the earth, that accounts for 16 x 10^22 joules.
The excess energy is going somewhere and it doesn't always have to be reflected in an atmospheric temperature rise.
To make an analogy consider the following scenario.
Lots of people understand how the heat sink works that is attached to the CPU inside a PC. What the sink does is combat the temperature rise caused by the electrical current being injected into the chip. That number multiplied by the supply voltage gives a power input specified in watts. Given a large enough attached heat sink, the power gets dissipated to a much large volume before it gets a chance to translate quickly to a temperature rise inside the chip. Conceivably, with a large enough thermal conductance and a large enough mass for the heat sink, and an efficient way to transfer the heat from the chip to the sink, the process could defer the temperature rise to a great extent. That is an example of a transient thermal effect.
The same thing is happening to the earth, to an extent that we know must occur but with some uncertainty based on the exact geometry and thermal diffusivity of the ocean and the ocean/atmospheric interface. The ocean is the heat sink and the atmosphere is the chip. The difference is that much of the input power is going directly into the ocean, and it is getting diffused into the depths. The atmosphere doesn't have to bear the brunt of the forcing function until the ocean starts to equilibrate with the atmosphere's temperature. This of course will take a long time based on what we know about temporal thermal transients and the Fickian response of temperature due to a stimulus.

No comments:
Post a Comment